Madaline (Multiple Adaptive Linear Neuron) :
- The Madaline(supervised Learning) model consists of many Adaline in parallel with a single output unit. The Adaline layer is present between the input layer and the Madaline layer hence Adaline layer is a hidden layer. The weights between the input layer and the hidden layer are adjusted, and the weight between the hidden layer and the output layer is fixed.
- It may use the majority vote rule, the output would have an answer either true or false. Adaline and Madaline layer neurons have a bias of ‘1’ connected to them. use of multiple Adaline helps counter the problem of non-linear separability.
Architecture:
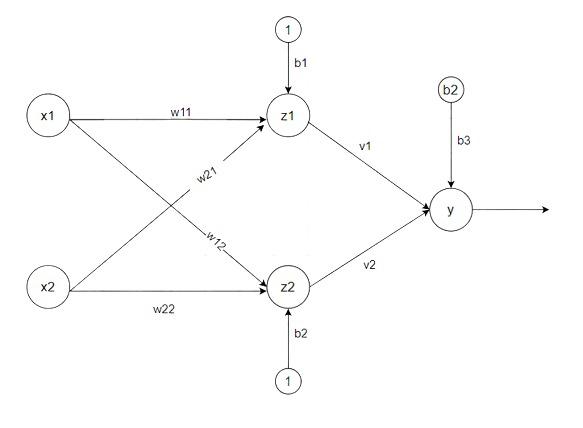
Madaline
There are three types of a layer present in Madaline First input layer contains all the input neurons, the Second hidden layer consists of an adaline layer, and weights between the input and hidden layers are adjustable and the third layer is the output layer the weights between hidden and output layer is fixed they are not adjustable.
Algorithm:
Step 1: Initialize weight and set learning rate α.
v1=v2=0.5 , b=0.5
other weight may be a small random value.
Step 2: While the stopping condition is False do steps 3 to 9.
Step 3: for each training set perform steps 4 to 8.
Step 4: Set activation of input unit xi = si for (i=1 to n).
Step 5: compute net input of Adaline unit
zin1 = b1 + x1w11 + x2w21
zin2 = b2 + x1w12 + x2w22
Step 6: for output of remote Adaline unit using activation function given below:
Activation function f(z) =.
z1=f(zin1)
z2=f(zin2)
Step 7: Calculate the net input to output.
yin = b3 + z1v1 + z2v2
Apply activation to get the output of the net
y=f(yin)
Step 8: Find the error and do weight updation
if t ≠ y then t=1 update weight on z(j) unit whose next input is close to 0.
if t = y no updation
wij(new) =wij(old) + α(t-zinj)xi
bj(new) = bj(old) + α(t-zinj)
if t=-1 then update weights on all unit zk which have positive net input
Step 9: Test the stopping condition; weights change all number of epochs.
Problem: Using the Madaline network, implement XOR function with bipolar inputs and targets. Assume the required parameter for the training of the network.
Solution :
- Training pattern for XOR function :
- Initially, weights and bias are: Set α = 0.5
[w11 w21 b1] = [0.05 0.2 0.3]
[w12 w22 b2] = [0.1 0.2 0.15]
[v1 v2 v3] = [0.5 0.5 0.5]
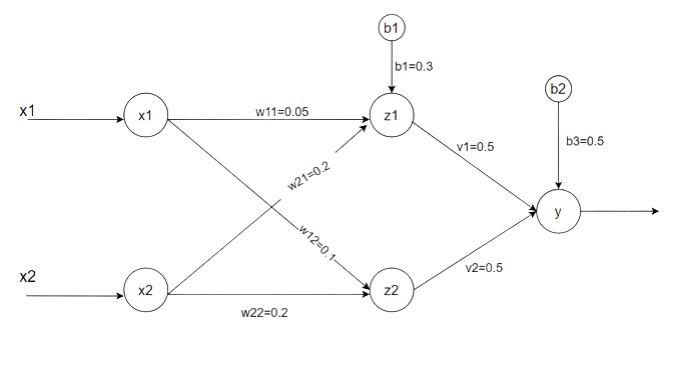
Madaline
- for the first i/p & o/p pair from training data :
x1 = 1 x2 = 1 t = -1 α = 0.5
- Net input to the hidden unit :
zin1 = b1 + x1w11 + x2w21 = 0.05 * 1 + 0.2 *1 + 0.3 = 0.55
zin2 = b2 + x1w12 + x2w22 = 0.1 * 1 + 0.2 *1 + 0.15 = 0.45
- Apply the activation function f(z) to the net input
z1 = f(zin1) = f(0.55) = 1
z2 = f(zin2) = f(0.45) = 1
- computation for the output layer
yin = b3 + z1v1 + z2v2 = 0.5 + 1 *0.5 + 1*0.5 = 1.5
y=f(yin) = f(1.5) = 1
- Since (y=1) is not equal to (t=-1) update the weights and bias
wij(new) =wij(old) + α(t-zinj)xi
bj(new) = bj(old) + α(t-zinj)
- w11(new) = w11(old) + α(t-zin1)x1 = 0.05 + 0.5(-1-0.55) * 1 = -0.725
w12(new) = w12(old) + α(t-zin2)x1 = 0.1 + 0.5(-1-0.45) * 1 = -0.625
b1(new) = b1(old) + α(t-zin1) = 0.3 + 0.5(-1-0.55) = -0.475
w21(new) = w21(old) + α(t-zin1)x2 = 0.2 + 0.5(-1-0.55) * 1 = -0.575
w22(new) = w22(old) + α(t-zin2)x2 = 0.2 + 0.5(-1-0.45) * 1 = -0.525
b2(new) = b2(old) + α(t-zin2) = 0.15 + 0.5(-1-0.45) = -0.575
So, after epoch 1 weight like :
[w11 w21 b1] = [-0.725 -0.575 -0.475]
[w12 w22 b2] = [-0.625 -0.525 -0.575]